Sorting Algorithms II - Insertion Sort
As we covered in the last class, bubble sort is one of the most inefficient algorithms for sorting a list. This is for two reasons.
- Bubble sort has a time complexity of
O(n^2)because it loops throughn-kitems in the list forn-1passes. Multiply the number of passesO(n)by the number of iterations in each pass, alsoO(n), and you getO(n^2). - Bubble sort behaves exactly the same way no matter whether the list is already fully or partly sorted. This means its best case time complexity and its worst case time complexity are both
O(n^2).
The first reason is impossible to change without using a fundamentally different type of algorithm - i.e. one that doesn't rely on passes through the list. We'll cover different types of sorting algorithm in later classes. But the second reason is more promising. If we have a way to change bubble sort so that it performs fewer passes or iterations, then we might be able to reduce its time complexity.
Enter insertion sort. Insertion sort is an improved version of bubble sort which often runs with better time complexity.
1st Pass
Let's start with our array from last time.

Just like bubble sort, we'll compare the first two elements.

Since 9 is larger than 4, we swap them. Unlike bubble sort, we now start moving backwards through the array. Since we're already at the first element, this is the end of the first pass.

2nd Pass
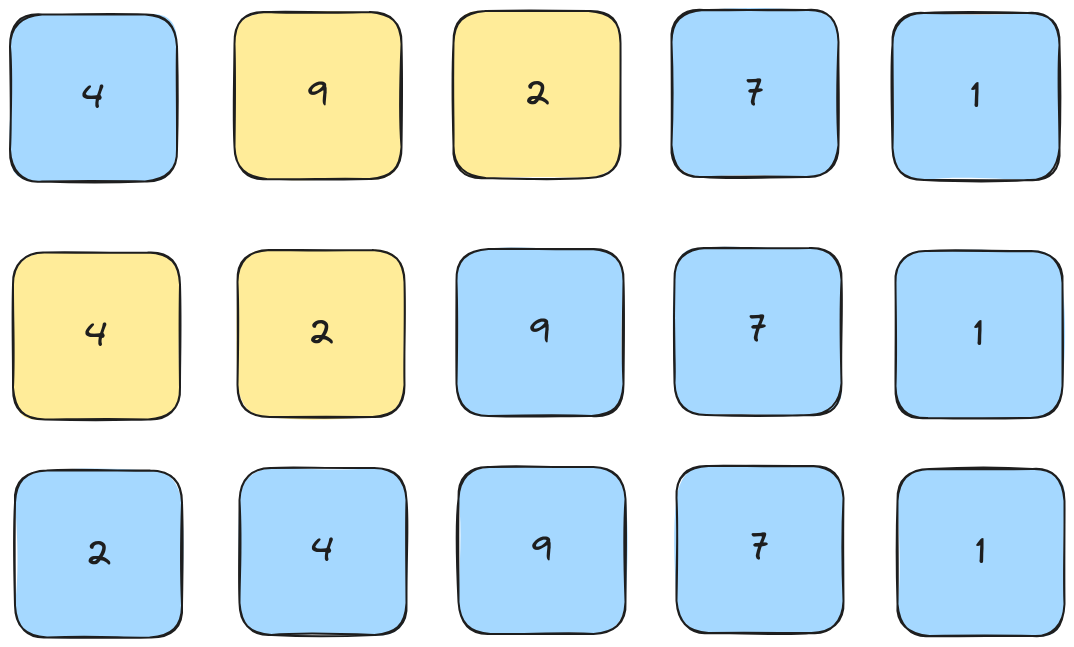
3rd Pass
Because 7 is already greater than 4, we finish this pass early. This is what makes insertion sort more efficient than bubble sort.

4th Pass
Unfortunately, 1 is the smallest number in the array, so this final pass is exactly the same as a full bubble sort.
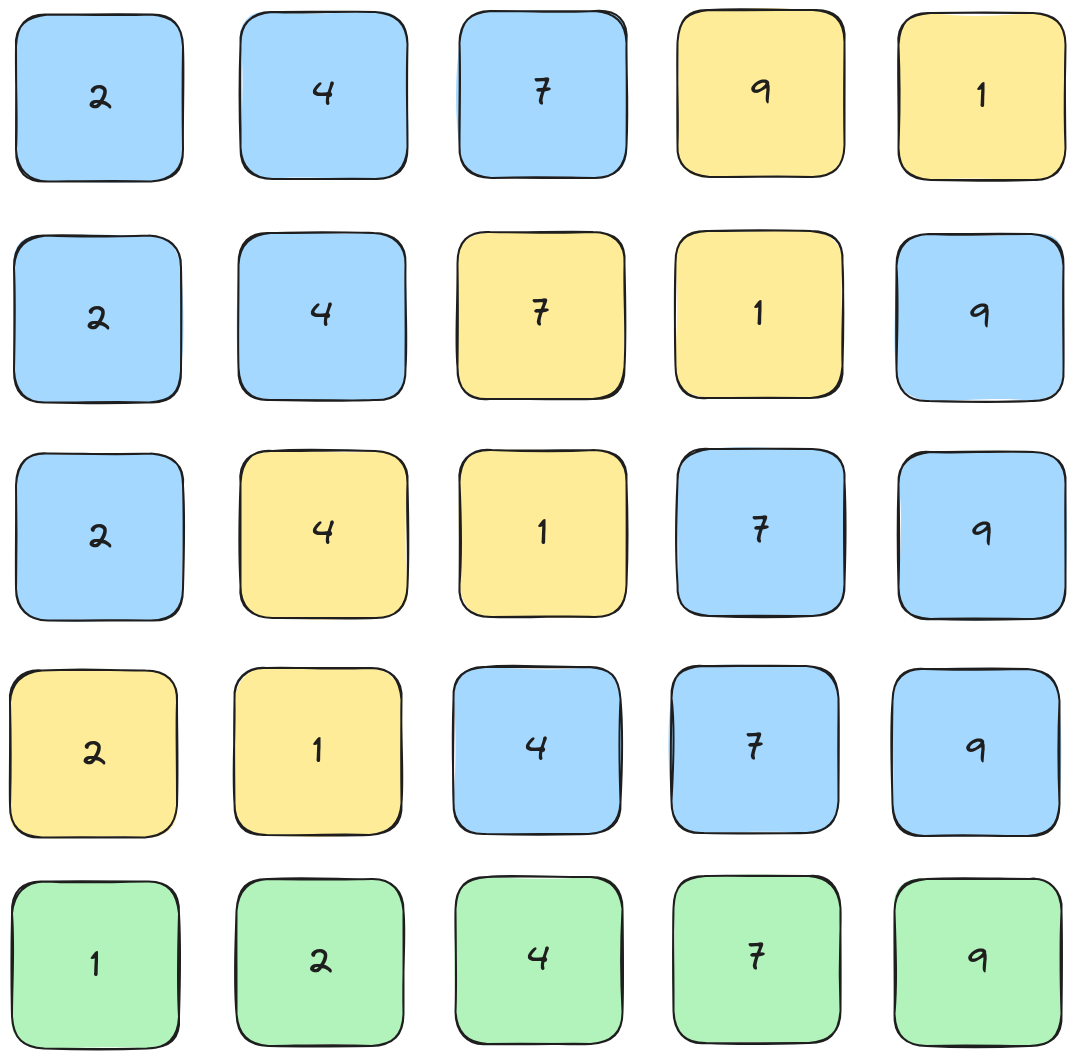
Questions
- Using index cards, post-it notes, or an app like Excalidraw, perform an insertion sort over the following lists:
[1,2,3,4,5][5,4,3,2,1]
- What is the best-case time complexity of insertion sort? What's the worst case? When do each of these happen?
- The most popular sorting algorithms in real-world use cases run in
O(nlogn)time. However, insertion sort is still widely used as a component of more complex, compound sorting algorithms. Can you think of a reason why this might be?
Assignment
- Write insertion sort in your language of choice, making use of the algorithm outlined above.
- Run both insertion sort and bubble sort across the following and record the real runtime using a tool like
time. What do you notice?- A list of 10000 elements in ascending order (i.e. already sorted).
- A list of 10000 elements in reverse order.
- Random lists of 10, 100, 10000, and 1 million elements.
Answers to Questions
- Practice exercise.
- The best-case time complexity of insertion sort is
O(n), which happens when the list is fully sorted. The worst case isO(n^2)which happens when the list is in reverse order, causing insertion sort to degenerate into bubble sort. - Because the best-case time complexity of insertion sort is
O(n), it's better than the most efficient competitors in cases where a list is already mostly or partly ordered. This is most likely to happen in lists with a small number of items. Therefore, insertion sort is often used to sort small lists when included as part of a compound sorting algorithm.