Sorting Algorithms I - Bubble Sort
Bubble sort is one of the most famous algorithms for sorting elements in a linear data structure such as an array. As we'll see later, it's also the least efficient. However, as bubble sort demonstrates most of the core principles of all sorting algorithms, it's worth reviewing.
1st Pass
Here is an array of 5 elements.

Compare the first two elements. If the first number is bigger than the second one, swap them.
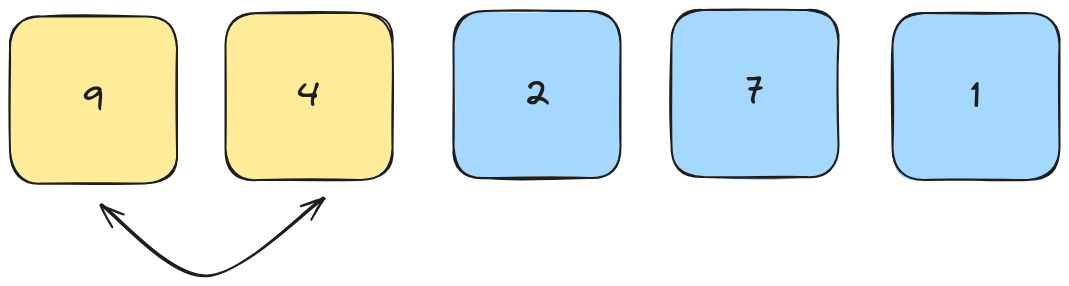
Repeat until the end of the array.



Now the last element is sorted, this is the end of the first pass.

2nd Pass
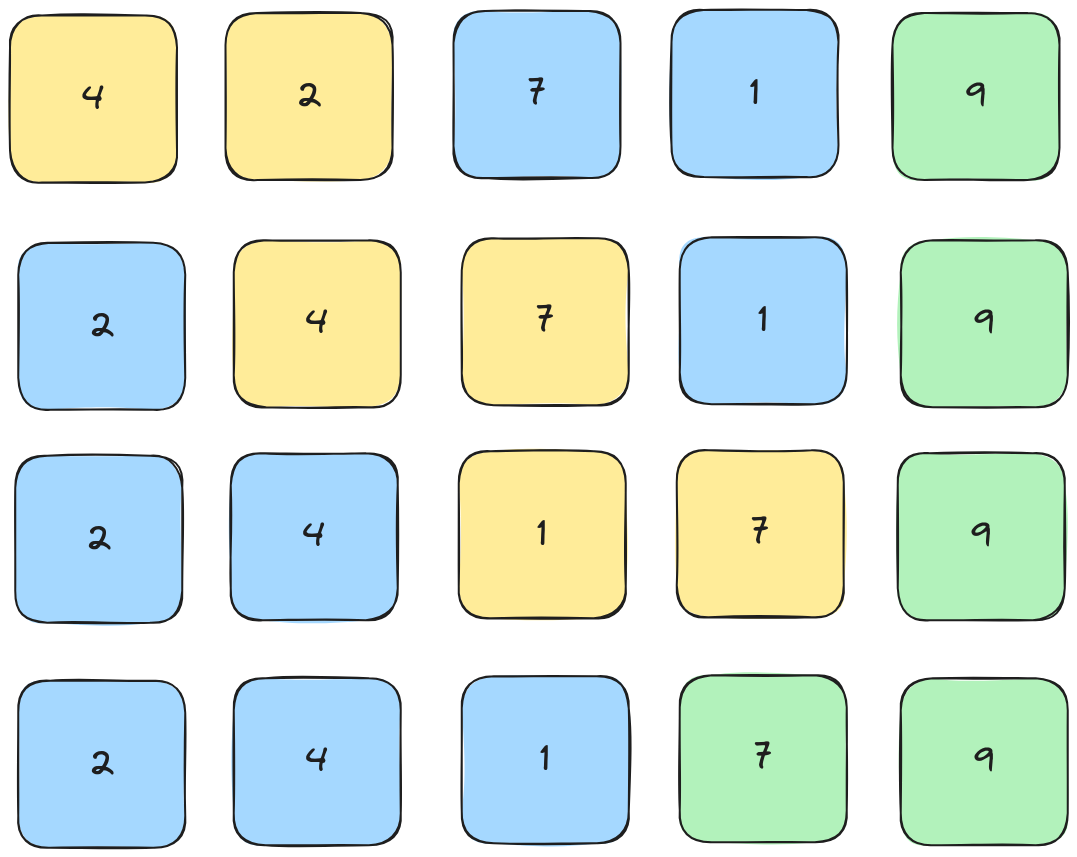
3rd Pass
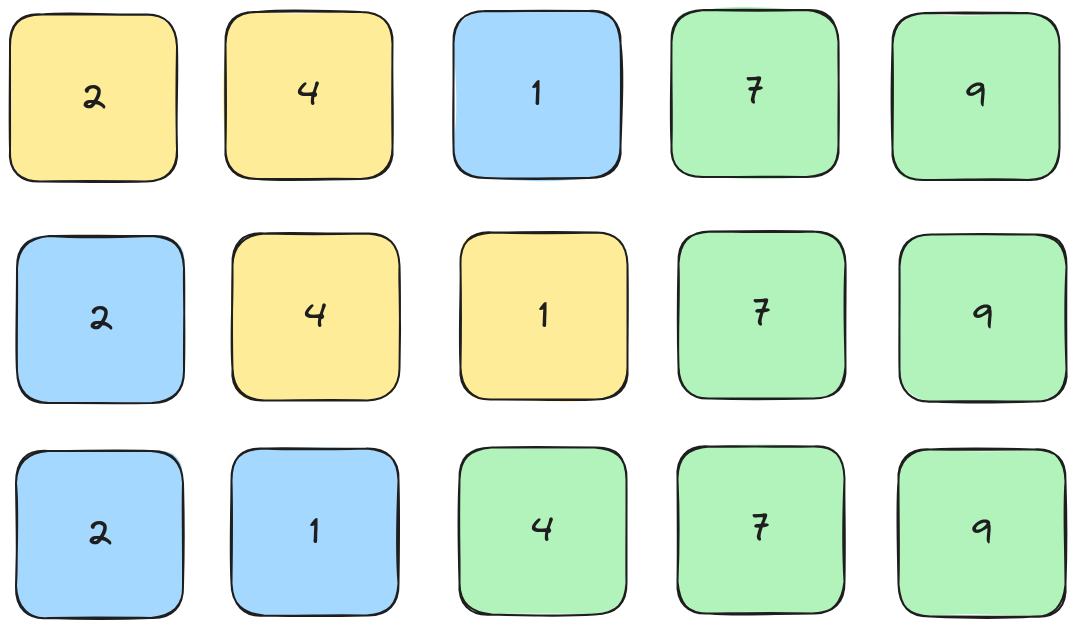
4th Pass
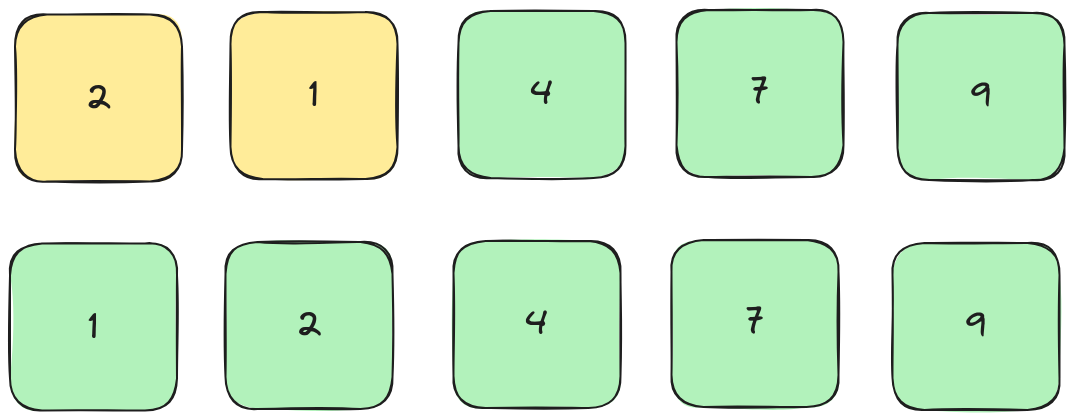
As you will have noticed, this is an extremely large number of steps (and a lot of computation) used to sort a very short array.
Questions
- How would you sort a list in descending order (i.e. the largest element first)?
- What's the best and worst case time efficiency of bubble sort as described above? Is there any difference between big O and T notation for this?
- Bubble sort is notoriously inefficient. But which part of this algorithm is the least efficient? Can you think of a way to improve it?
Assignment
Try writing the bubble sort algorithm over an array of integers. You can use any language you like but remember to follow the following steps:
- Select the next two elements of the array. Let the first be
aand the second beb. - If
ais higher thanb, swap their values. - Repeat until
ais the element at indexn-kwherekis the number of times we've repeated. - When
k == n, we've finished.
Extension 1: Try testing the runtime of the algorithm with arrays of the following sizes:
- 5 elements
- 20 elements
- 100 elements
- 1000 elements
- 1000000 elements
If you're on Linux, MacOS, or WSL you can use time for this.
Extension 2: Modify your algorithm so that it can sort the list in ascending or descending order.
Extension 3: We have a set of dictionaries with arbitrary values. For example:
objects = [
{'id': 1, 'a': 3, 'b': 1, 'c': 2},
{'id': 2, 'a': 2, 'b': 2, 'c': 3},
{'id': 3, 'a': 1, 'b': 3, 'c': 1},
]
Modify your algorithm so that it can sort these objects by any of the keys as provided in an external function.