Quicksort and Partition Schemes
Merge sort has many advantages over linear sorting algorithms. As we've covered, it's faster in the worst case than insertion or bubble sort: merge sort is O(nlog(n)) while both bubble and insertion sort are O(n^2). While it can sometimes be slower in the best case, this is an edge case which is resolved by compound sorting algorithms.
Merge sort also has several real-world advantages. For example, it's easy to parallelise and can be run against massive on-disk data sets. This makes it very suitable for sorting database tables and other large data stores. It's also relatively easy to implement, which makes it great for applications where implementation errors would have terrible consequences (e.g. databases).
One thing you might have noticed about merge sort is that it always runs in O(nlogn) time, even if the list it's given is already partly sorted. This is because it doesn't examine the list until after it's already split it into its individual elements. The best case, worst case, and average case of merge sort are all O(nlogn)!
Merge sort also requires additional space (memory or disk) to run the merge function. While it is possible to optimise this additional space usage, it's not possible to completely eliminate it.
It would be great if we had an algorithm which could help with these two issues. Enter quicksort. It's a recursive sorting algorithm, like merge sort, but it addresses both the space requirements of mergesort and its low efficiency over sorted lists.
How Quicksort Works
The main concept in quicksort is the pivot. This is a single element which we use to partition our input for sorting. You can choose any element of the list as the initial pivot and the algorithm will work. In this case, we're using the last element of the list.
Which element of the list we choose as our pivot is relevant to our partition scheme, which we'll discuss later. We're currently using the Lomuto partition algorithm.
Our goal is to place numbers which are smaller than the pivot to the left (before) the pivot, and numbers which are greater than the pivot after it.
We do this by moving numbers that are smaller than the pivot to the left-hand side of the list, then moving the pivot so it's after them. To do this we need to use a pointer to keep track of the list. This pointer will start at the start of the list.
Here's a familiar list of numbers.
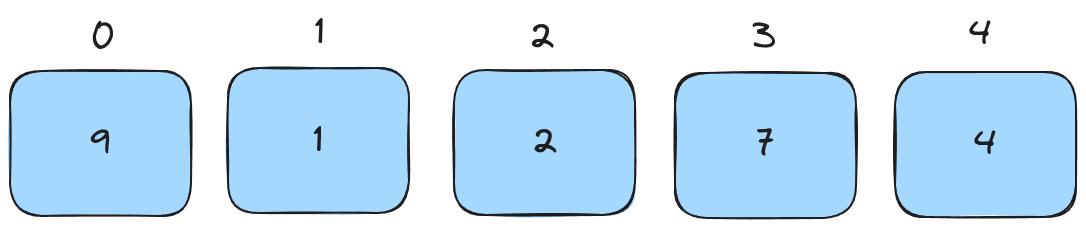
We select one element to be the pivot. In this case, it's the last element of the list.
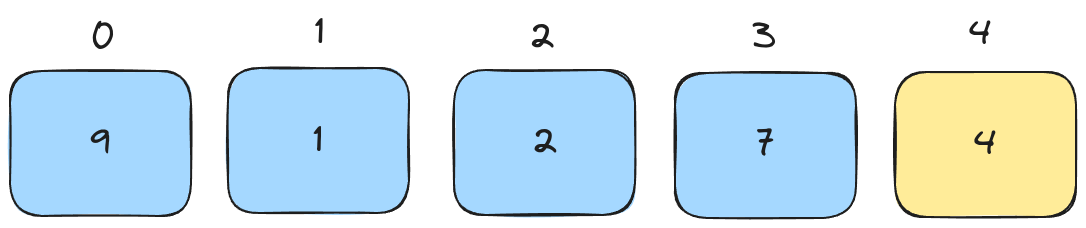
Compare the pivot with the pointed element.

Keep checking elements. If the element is smaller than the pivot, swap it with the pointed element from earlier, and increment the pointer.
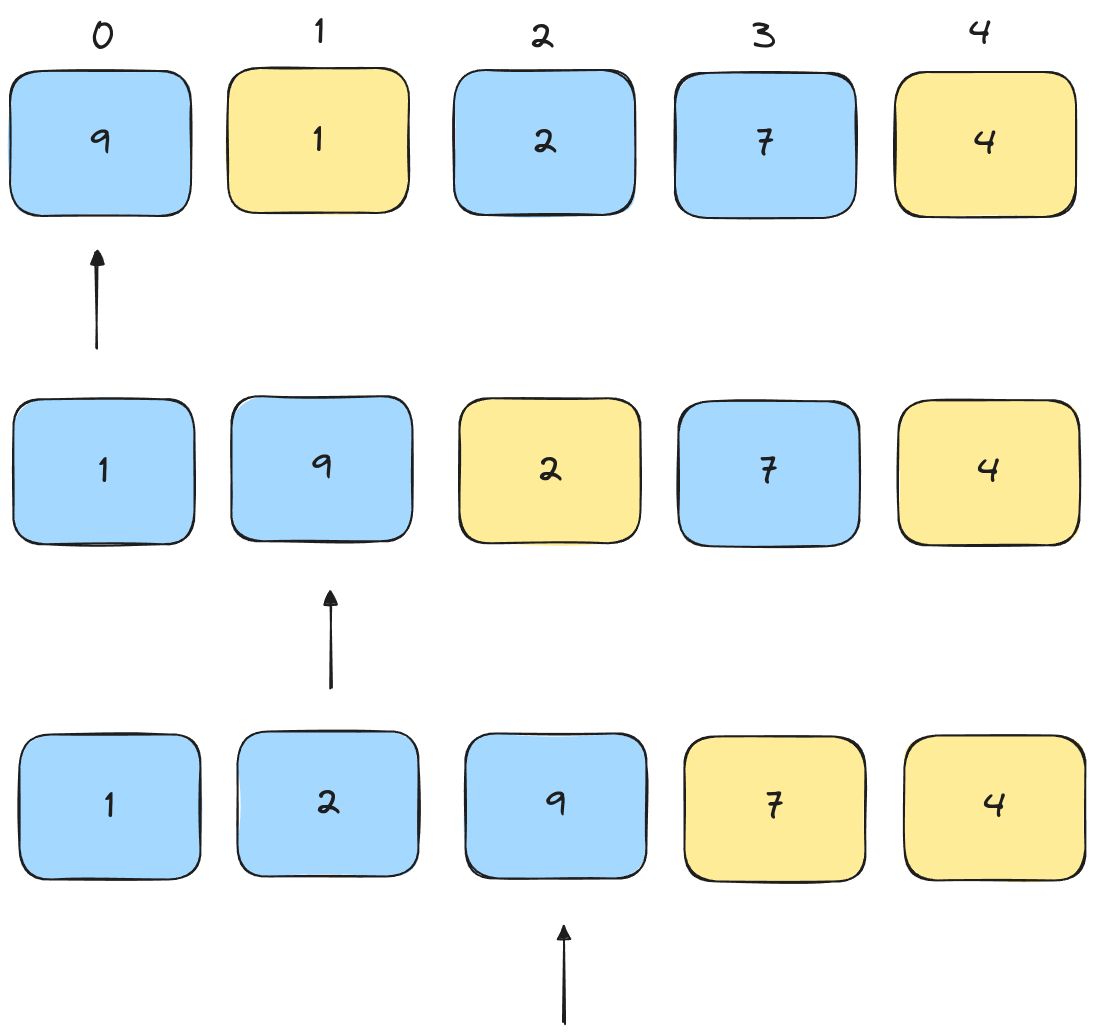
Finally, swap the pivot with the pointed element.
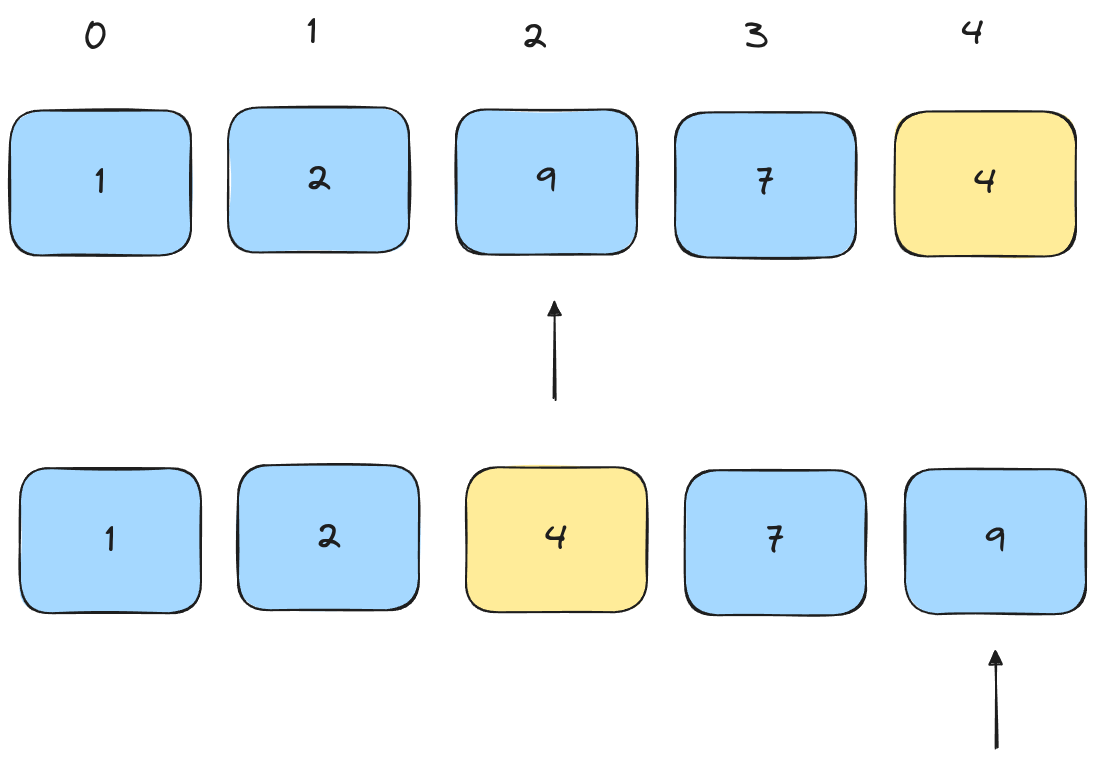
Wow! Our list is already sorted! However, this is not the end. We don't yet know that the list is sorted - all we know is that the pivot is in the correct place. To finish sorting we need to partition the array around the pivot and run quicksort again for the list on each side of the pivot.
Let's try it again for the left-hand side of the list. We check the first element (1) against the pivot (2):
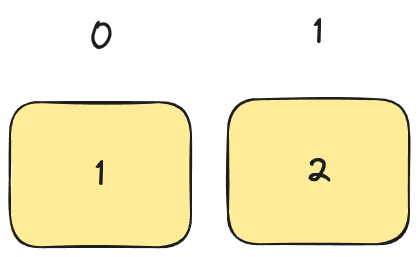
As the first element in the list is smaller than the pivot, we swap it with itself and increment the pointer. Finally, we swap the pivot with the pointed element (which is also the pivot). There is no change to the array from all of this.
The same case occurs on the right hand side of the list.
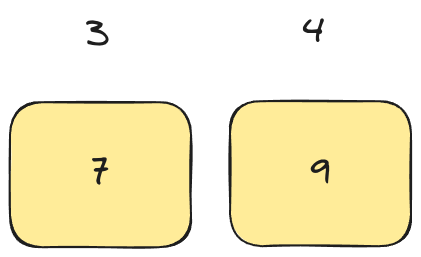
The last two recursions are into arrays of one element, so they are already sorted. We finish recursing, and our array is fully sorted.
Problems
- Implement quicksort over a list of 100 random numbers. You may use any language that's comfortable for you, but I recommend Python (more similar to pseudocode) or a low level language like C, C++, Go, or Rust (more direct impact on performance). A reference is provided at the base of the
- Compare the performance of merge sort against the performance of quicksort for lists of 10, 1000, 1m, and 100m random integers. You can use the UNIX
timetool, your IDE's built-in timer or a language-specific timer like Python'stime.perf_counter.
Time Analysis of Quicksort
Last class we covered the Master Theorem and Master Method. This lets us calculate a time complexity for any recursive algorithm, provided that sub-problems have the same structure as the original problem.
The problem we're solving in quicksort is placing the pivot in the correct location. We then do this recursively until we reach a list with only one element. So quicksort meets the requirements for analysis with the Master Theorem.
Let's recap the Master Theorem:
For an equation of the form T(n) = aT(n/b)+O(n^d):
a = b^d => T(n) = O((n^d)logb(n))
a < b^d => T(n) = O(n^d)
a > b^d => T(n) = aT(n/b)+O(n^d)
How do we give a value to the variables a, b, and d in the case of quicksort? a and b are simple: we split the input in half (excluding the pivot), then run quicksort twice, once for each half of the input. So a=2 and b=2 for quicksort. As we scan through the list one time per problem (to place the pivot), intuitively d=1. Therefore, for quicksort:
a=2,b=2,d=1
b^d = 2
So a = b^d
T(n) = O(n^1 * log2(n))
T(n) = O(nlog2(n))
This is the correct answer for the average case of quicksort (for more on why this is the case, see here).
However, for quicksort this is not the whole story. The worst-case and the average-case are different!
Let's examine a list that looks like this. We use the familiar lomuto partition scheme and pick our pivot as the last element.
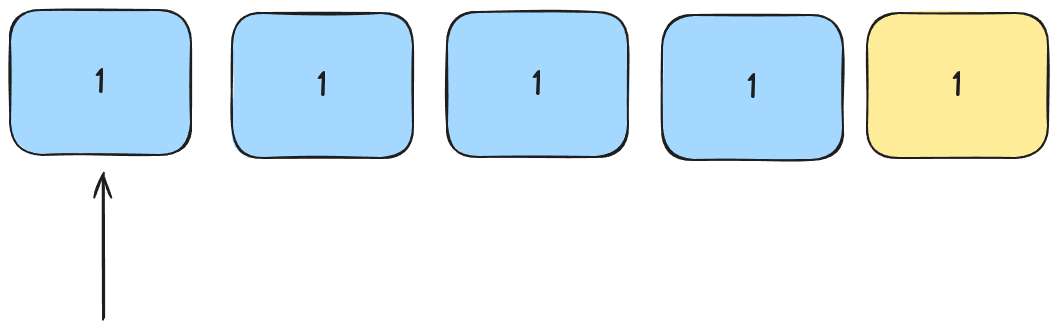
Since no element is smaller than the pivot, we swap the pivot with the first element in the list and continue with our right-hand sub-array:
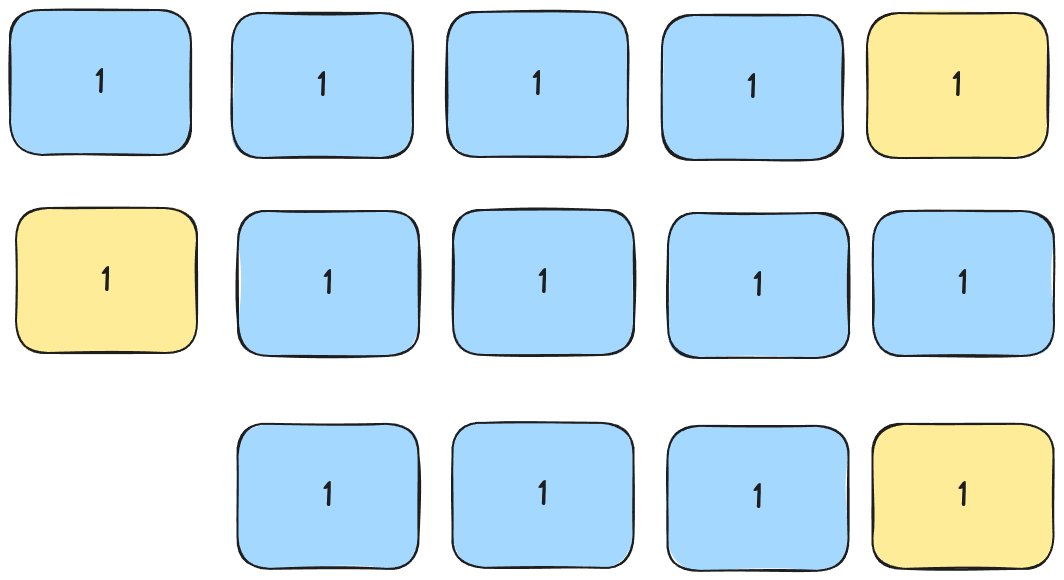
This continues until we only have a single element in our sub-array.
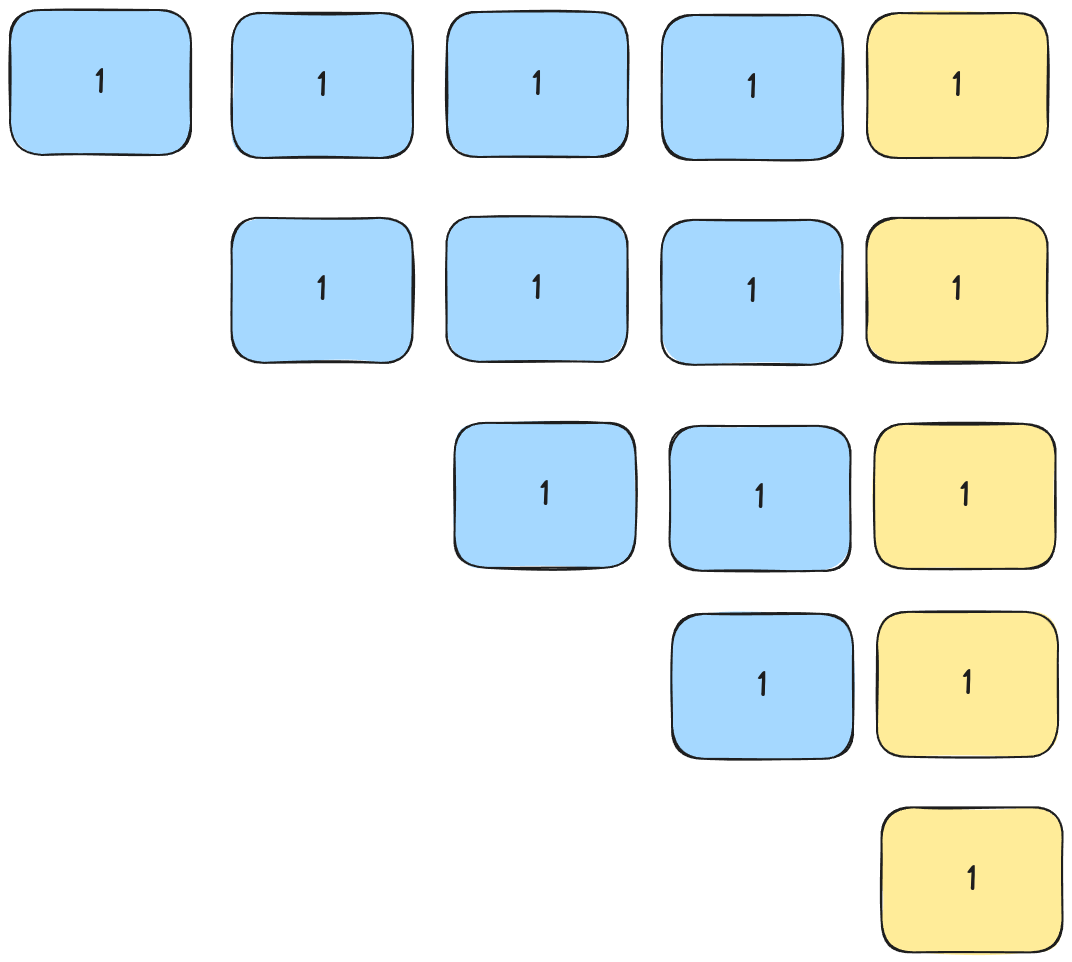
In order to 'sort' this list of 5 numbers we need to run quicksort 5 times. And recall that every time we have to compare each element to the pivot. Our time complexity is:
T(n) = n + (n - 1) + (n - 2) + (n - 3) ...
By arithmetic summation:
T(n) = n/2(n-1 + 0)
T(n) = (n^2 - n) / 2
T(n) = O(n^2)
Our worst case time complexity for quicksort is O(n^2). This doesn't just happen when we have a list of identical numbers, but in any situation where the pivot is consistently the largest or smallest number. In real-world implementations of quicksort we often choose a random pivot to avoid this.
To implement a random pivot, we can choose a random number, move it to where the pivot would normally be, and return it to the correct position after partitioning is complete.
Other Partitioning Schemes
There are other partitioning schemes aside from the Lomuto partition. The most common of these is the Hoares partition scheme.
While in the Lomuto partition we work from the left, swapping numbers as we go, in the Hoares partition we use pointers on the left and right simultaneously. Our pivot is set to the first element in the list.
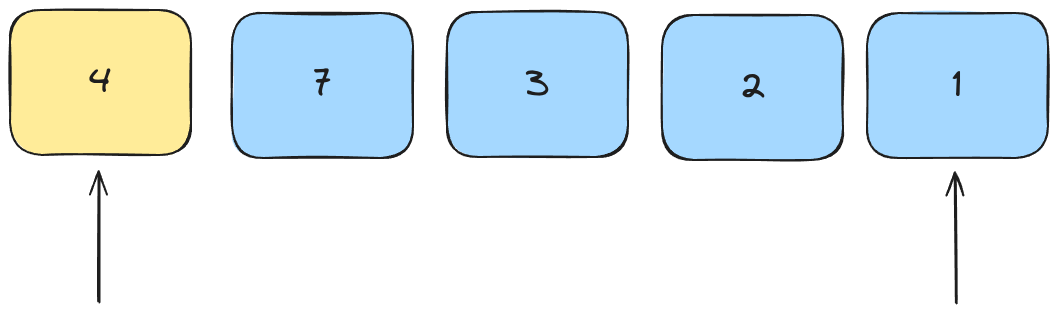
We find the leftmost element that's greater than the pivot, and the rightmost element that's less than the pivot.
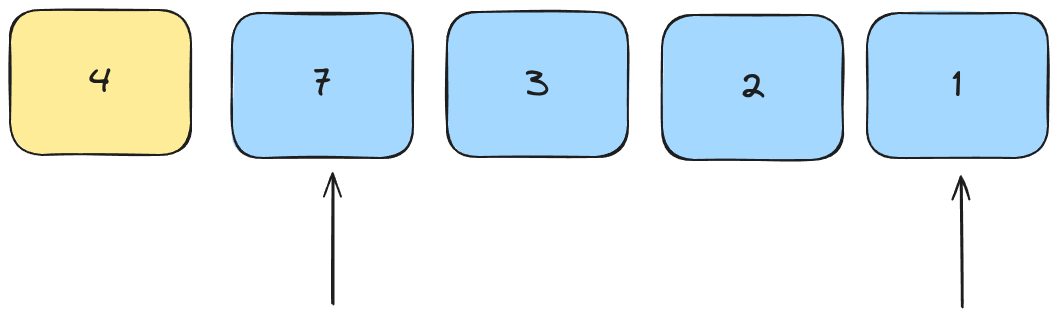
We swap them and keep going.

When the two pointers meet, we've found the correct position for the pivot! Finally we can swap the pivot with this element.
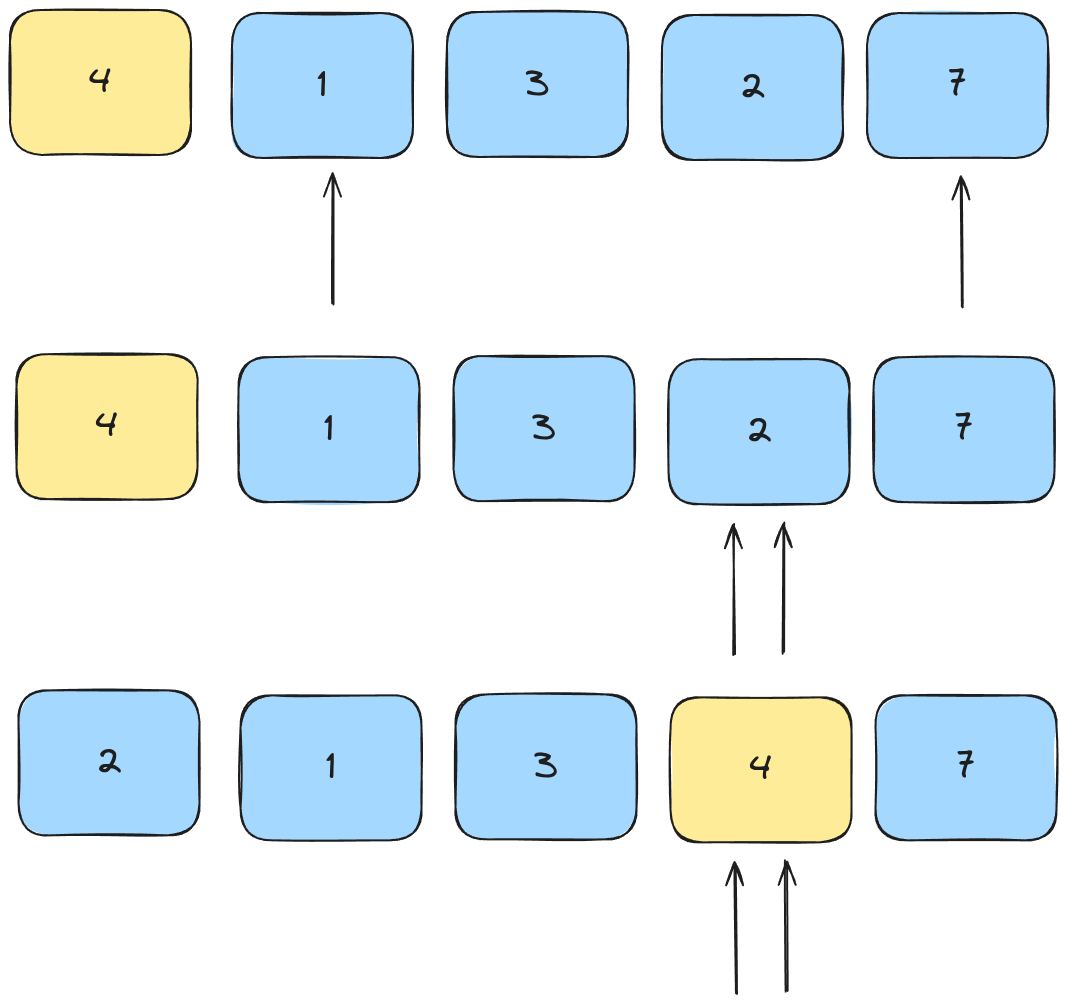
While this is bit less intuitive than the Lomuto partition, by the end of the partition we have successfully placed all elements smaller than the pivot to its left, and all elements greater than the pivot to its right.
Quick Sort vs Merge Sort
In many real-life cases quick sort is faster than merge sort, as we can intuit from the original demo. However, as we've seen, if the pivot is selected badly, then quick sort is substantially slower than merge sort. Therefore we need to take care to select our data sets if we want to use quick sort effectively.
Another property of quick sort is that it's an unstable sort algorithm - it will swap numbers even if they have the same value (i.e. it'll swap the pivot and the pointed number). This can lead to unnecessary computation.
Another issue with quick sort in the real world is that it requires fast random access to the list. This is fine when we're working on lists that fit in RAM, but a lot more complex when working on disk. Hard disks are still cheaper for large amounts of storage space as of 2024, and deal poorly with random access. Although SSDs and other flash-based storage have much better random access speeds, random access still has a penalty compared to linear access.
Finally, quicksort is prone to off-by-one errors in implementation - which can lead to memory safety problems in low-level languages - and can be 'attacked' by feeding it data sets that force it into n^2 time complexity. This can make it a poor choice where security is a major concern.
For these reasons, merge sort is often used instead of quicksort in the real world.
what we really need is an algorithm with the benefits of quicksort, but without its stability issues. Next time we'll cover a compound sorting algorithm which makes use of multiple sorting techniques to achieve this: timsort!
Review Questions
Answers at the end of this article. These are the key points of the class.
- What is the primary approach of quicksort to sorting a list?
- What's the average-case time complexity of quicksort?
- What's the worst-case time complexity?
- What's the main difference between Hoares and Lomuto partition schemes?
- Are quicksort or merge sort more suitable for sorting the following? Why?
- National health records
- A list of 1000 books in a school library
- The global interaction data for users on Facebook today
Assignment
- Implement quicksort using the Hoares partition scheme.
- Implement a random pivot for the partition algorithm of your choice.
Reference Implementation
This reference implementation includes both Hoares and Lomuto partition schemes, which you can experiment with by changing the hoares flag.
As quicksort implementations are prone to off-by-one errors, I've provided example so that you have a known good source to work from and study.
import random
def generate_list(length : int, min : int = 1, max : int = 10000):
return [random.randint(min,max) for i in range(length)]
def swap(arr, i1, i2):
tmp = arr[i1]
arr[i1] = arr[i2]
arr[i2] = tmp
def lomuto_partition(arr, lower, upper):
# let pivot be the far-right value
pivot = arr[upper]
# let i start to the left of lower (so that on increment it's at lower)
i = lower - 1
# for everything between indexes lower and upper
# if something is less than pivot
# then put it in the next available left-hand slot (pointed by i)
for j in range(lower, upper):
if (arr[j] < pivot):
i += 1
swap(arr, i, j)
# swap pivot with whatever's pointed by i (the next left hand slot)
swap(arr, i+1, upper)
# return position of pivot
return i+1
def hoares_partition(arr, lower, upper):
pivot = arr[lower]
# i.e. to the left of the lower bound
i = lower - 1
# i.e. to the right of the upper bound
j = upper + 1
# Basically, move the left and right pointers towards each other, swapping numbers in the wrong place
# The goal is to place all numbers smaller than the pivot to the left of it
while (True):
# Find first element >= pivot
i += 1
while (arr[i] < pivot):
i += 1
# Find last element <= pivot
j -= 1
while (arr[j] > pivot):
j -= 1
# If they're at the same position, we found the pivot!
if (i >= j):
return j
swap(arr, i, j)
def quicksort(arr, lower, upper, hoares = True):
# choose the appropriate partition scheme based on input
partition_fn = hoares_partition if hoares else lomuto_partition
if lower < upper:
# sort and find the pivot point of the partition
pivot_i = partition_fn(arr, lower, upper)
# hoares and lomuto take slightly different parameters; adjust left upper bound for the different schemes
next_upper = pivot_i if hoares else pivot_i - 1
# sort left of pivot
quicksort(arr, lower, next_upper, hoares)
# sort right of pivot
quicksort(arr, pivot_i + 1, upper, hoares)
def main():
arr = generate_list(10, 1, 10)
print(f'Unsorted: {arr}')
quicksort(arr, 0, len(arr) - 1, True)
print(f'Sorted: {arr}')
if __name__ == "__main__":
main()
Answers / Summary
- Quicksort's primary approach is to partition an input array using a pivot, such that elements smaller than the pivot are to its left and elements larger than the pivot are to its right. It repeats this recursively until all elements are correctly placed.
- The average case time complexity of quicksort is
O(nlogn). - The worst case time complexity is
O(n^2). - The main difference is that in the Lomuto scheme, we maintain pointers only on the left side of our input, while in the Hoares scheme, we maintain pointers to both ends of the input.
- These are suggested answers:
- National health records should probably be sorted with Merge Sort for security reasons and possibly scale.
- A list of 1000 books is very small amounts of data and non-critical, so quicksort is fine.
- The daily interactions on a large social media platform are massive, so merge sort is likely necessary to make efficient use of computing resources.