Sorting Algorithms III - Merge Sort
So far, all the sorting algorithms we've covered have been iterative -- they make at least one pass through a list, then swap items until the list is fully sorted. This makes them very difficult to optimise, both from an algorithmic perspective and in practical engineering terms.
In algorithmic terms, if we're making multiple passes through a list and performing new iterations every time, our worst case scenario cannot be better than O(n^2).
In practical engineering terms, we have an issue with our order of operations. Recall the order that bubble and insertion sort operate in:
- We make a pass from one end of a list to the other, swapping elements as we go.
- We repeat (1) until the list is fully sorted.
This means that operations are serial - we need to wait on the result of the previous pass before we can compute the next part. Modern computers often have 4 or more CPU cores and hundreds of GPU cores. If we are able to run our operations in parallel on multiple cores, we can likewise speed up our programs by a factor of 4 to thousands. (Note that this has no impact on our time complexity, as we still need the same number of operations, but it has a big impact on the real time used.)
Merge sort solves both of these problems by making a more efficient algorithm which can run across many machines or cores in parallel. Let's see how it works.
Here's a familiar array.

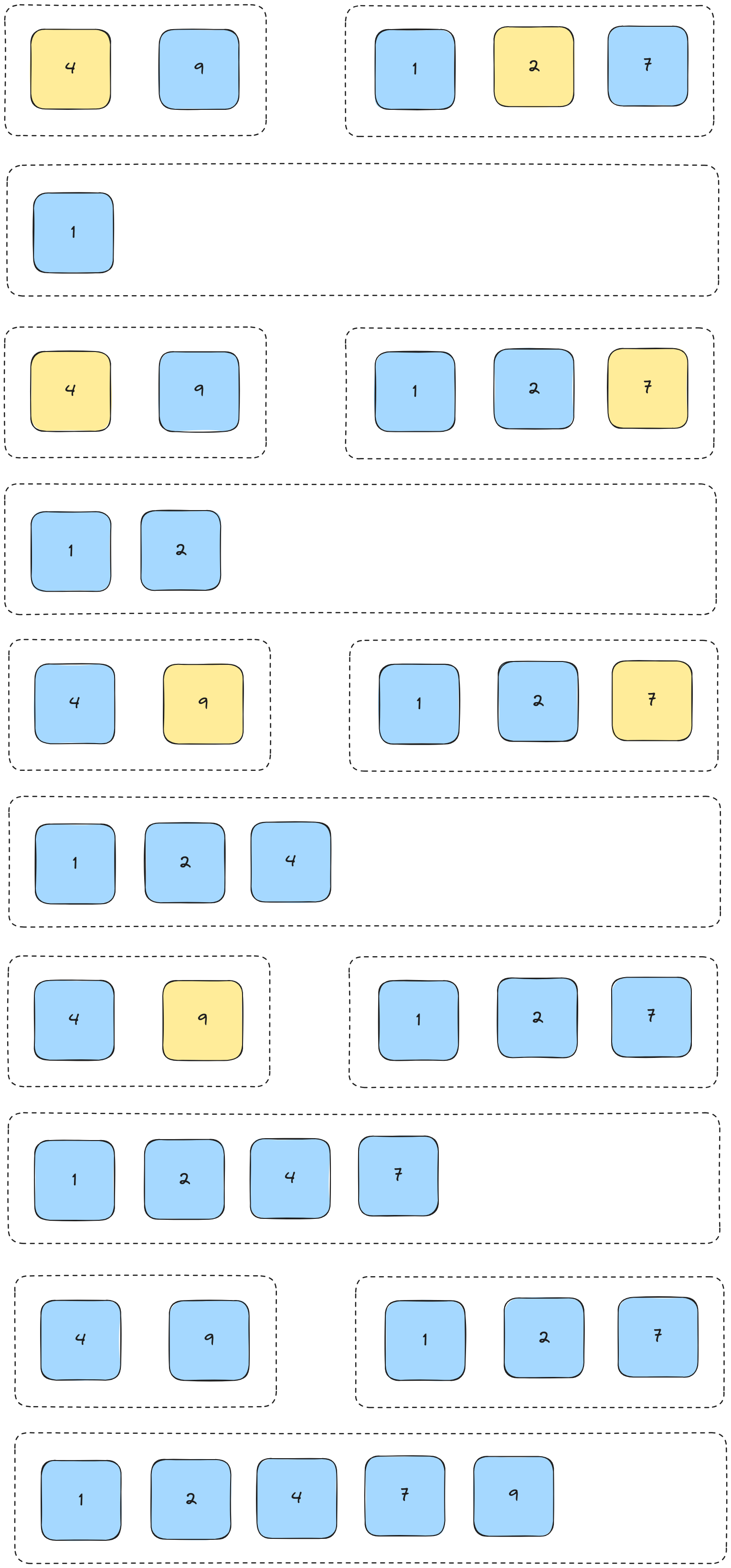
Phase 1: Split the array
We're going to split the array in half until we reach singular elements. Since we can't split a list of 5 elements exactly in half, we just go left of center by one.
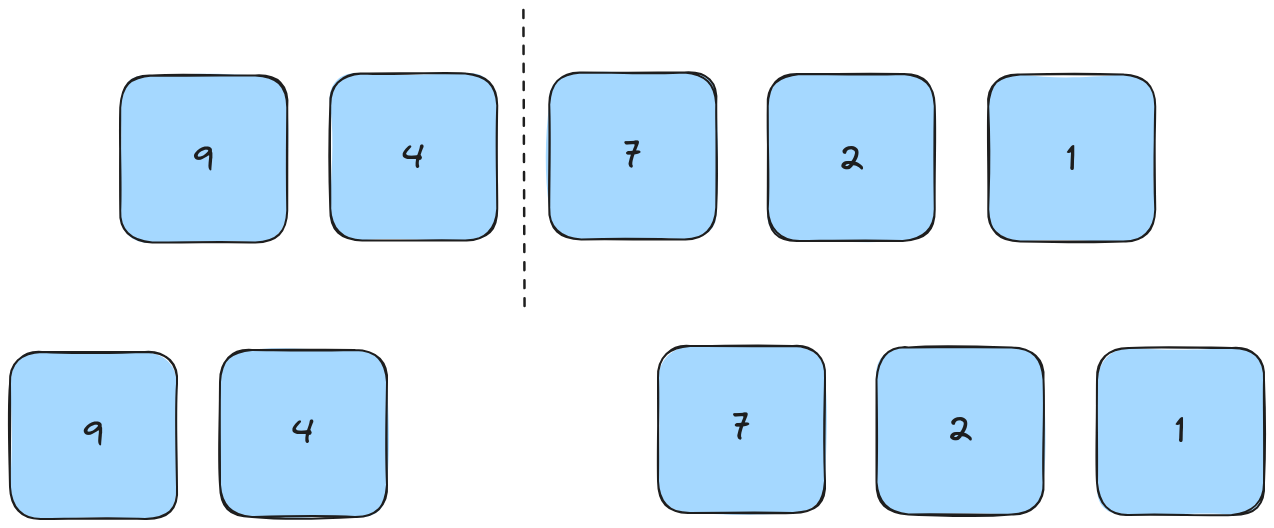
We then continue splitting by the same rules until we reach lists of only one element.
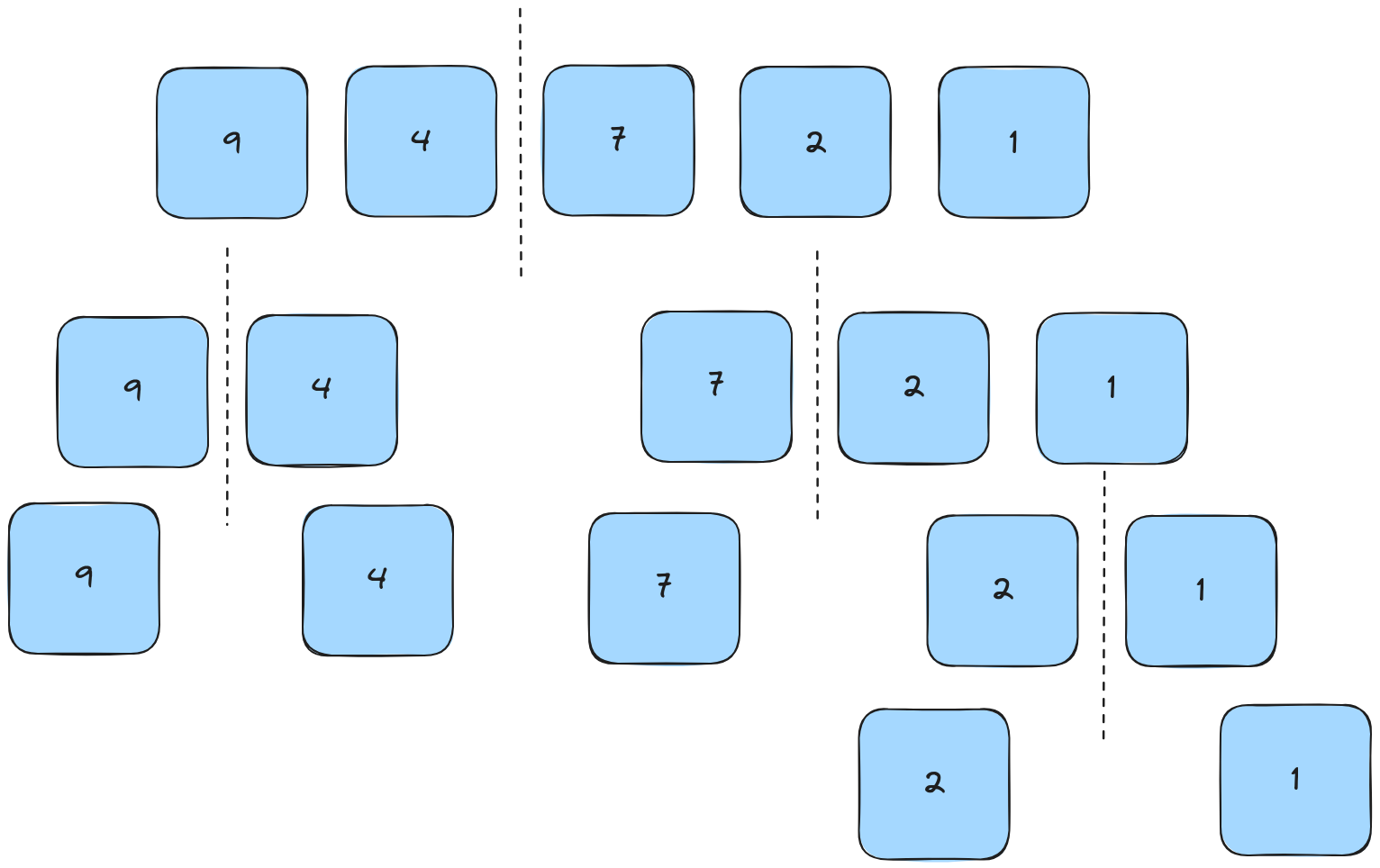
Phase 2: Recombine lists
We now start comparing lists in the same order we split them. We'll use the left-hand tree for this and go step-by-step.
First we compare the two elements and form a new list by enqueuing them in order.
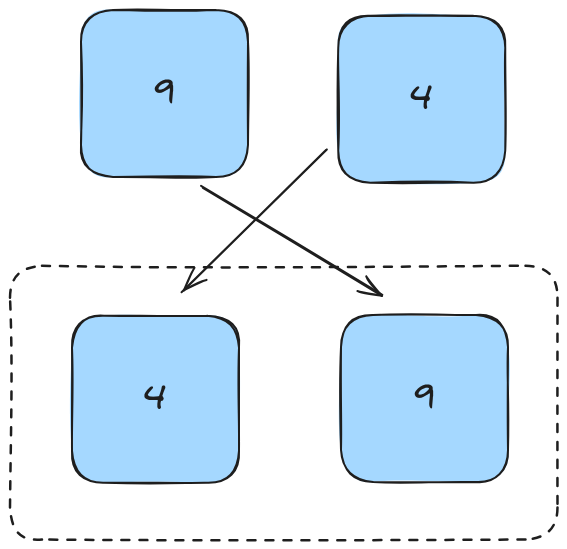
We then continue this process by setting up pointers for each sublist. As we're currently 1 level deep, the list we'll compare to is the sorted right hand side of the tree.

We compare each element from both lists and insert them into our new list (i.e. we merge them.
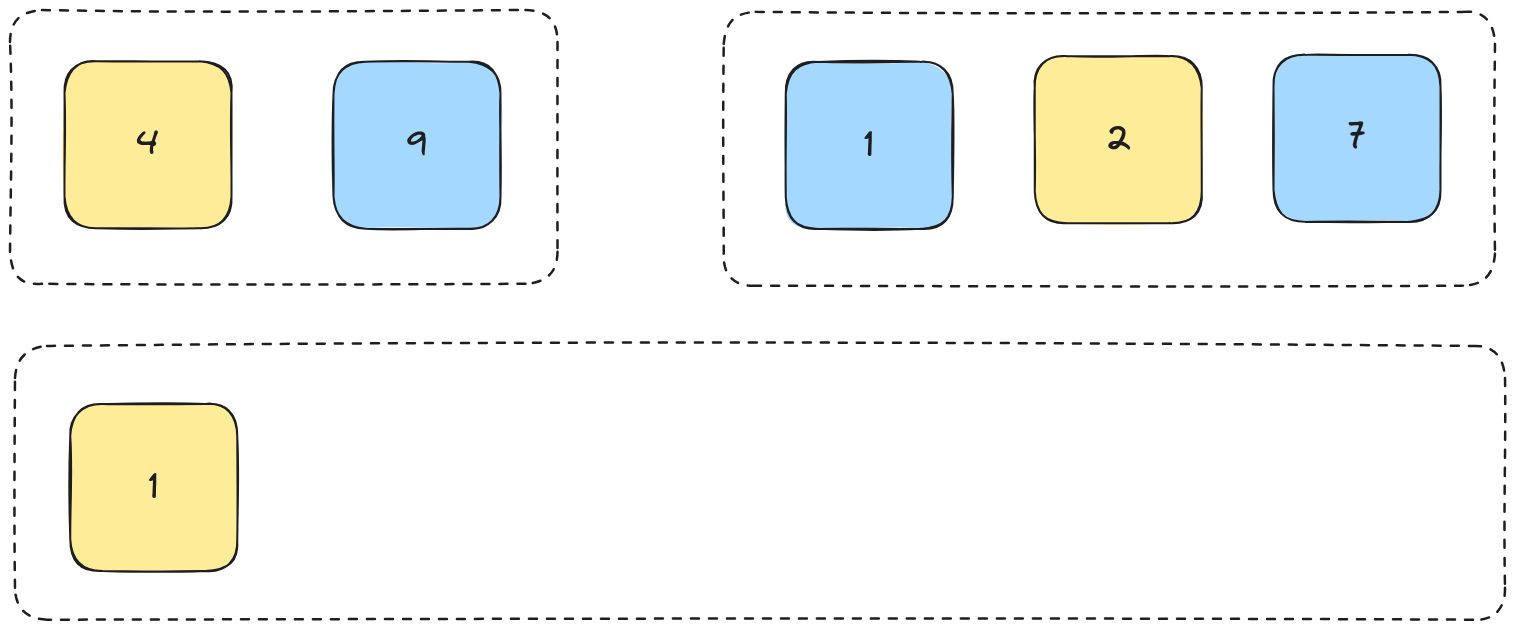
We then continue this process until the two lists are fully merged.
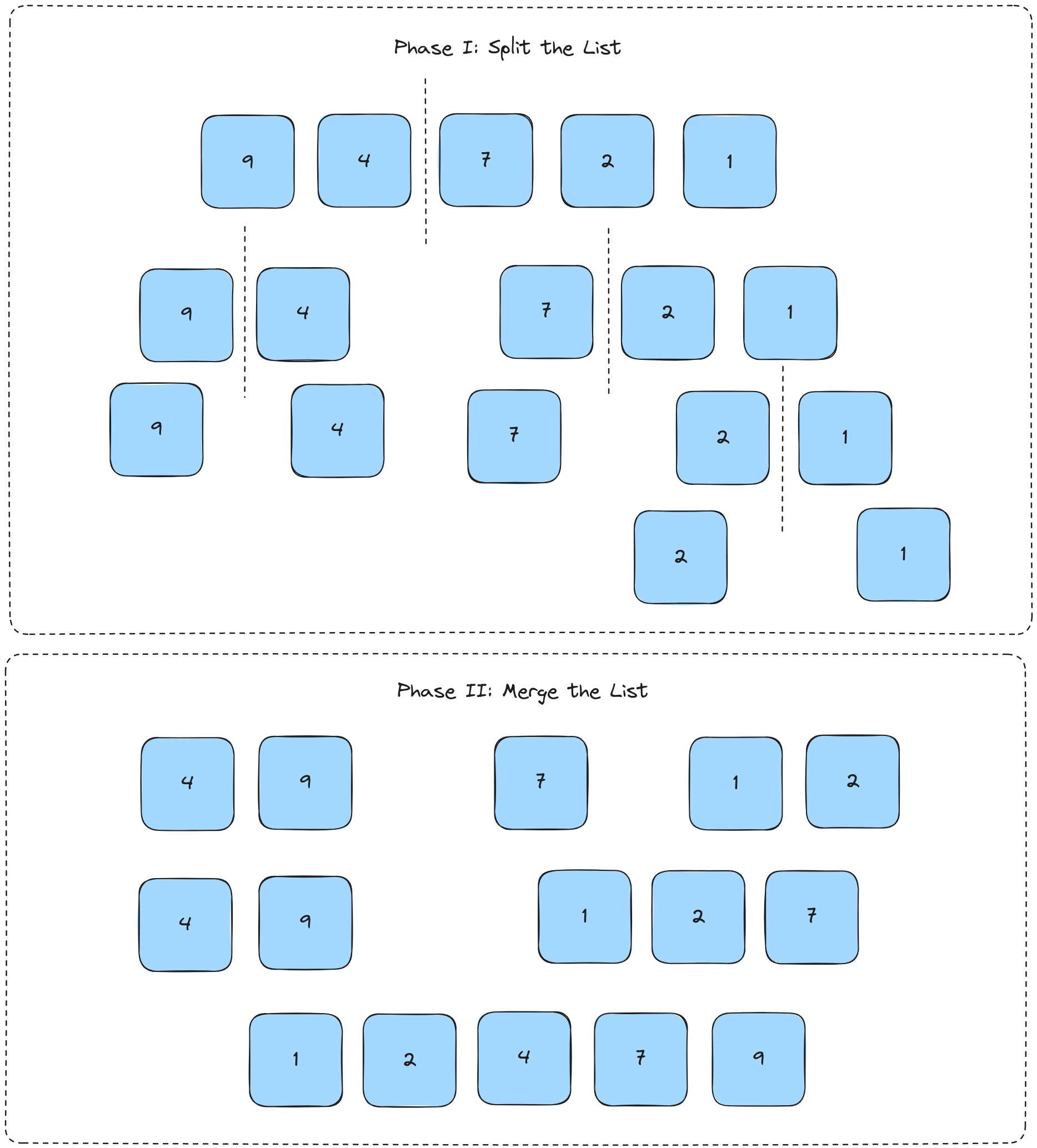
Here's an example of the full process of merging the lists, glossing over the step-by-step comparison for each list.
Assignment
In this class we're going to write the program first and then move onto theory questions.
Write a basic merge sort in the language of your choice. The simplest way to write it is by using a recursive algorithm, but it is also possible to implement merge sort iteratively.
Problems
- The time complexity of merge sort is
O(nlog(n))Why is this? - How can we construct a version of merge sort that doesn't require a new array at each step?
- What's the space complexity of merge sort in the following cases?
- We create a new array of length n at each recursion.
- We don't create a new array at each recursion (an in-place sort).
- How could we construct a version of merge sort that runs across
n / 2cores or worker machines?
Extensions
- Write a version of merge sort using an approach which doesn't require a new array at each step.
- Write a version of merge sort which can use any comparison function (e.g. to work on complex objects, or to sort in descending or ascending order).
- Write a version of merge sort which takes advantage of multiprocessing / threading capabilities. In Python you can use the
multiprocessinglibrary for this. If you know how to implement threaded code in another language such as Go then feel free to use this as well. - Benchmark your multi-threaded solution against the single-threaded solution we produced above.
Answers
Problem 1
The time complexity of merge sort is O(nlog(n)). We first break our lists down into sub-lists of 2 elements and compare them. We do this by subdividing our original list into half over and over again. This is exactly equivalent to log2(n).
When we recombine our small lists of elements, we need to scan through all elements in the two lists we are comparing to make sure they're in the correct order. This takes O(n) time.
n * log(n) is nlog(n).
Problem 2
We can do this by passing pointers to positions in our original list, rather than creating new sub-arrays:
def merge_sort(array, start_index, end_index):
# in python this will lead to the array being passed
# by reference rather than being copied
merge_sort(array, start_index, end_index / 2)
merge_sort(array, end_index / 2, end_index)
array = [8,7,6,5,4,3,2,1]
sort(array, start_index, end_index)
Problem 3
If we create a new sub-array at each recursion, we need to create as many elements as there are in the parent list each time we recurse (across all sub-lists). This is O(n) space complexity. We recurse O(log(n)) times as above. Therefore the space complexity of this merge sort is also O(nlog(n)).
If we do not create a new array at each step then merge sort takes O(1) space. This is because the only memory overhead for this kind of algorithm is the original array, which is not included, and pointers used to keep track of the current list. By not using a recursive algorithm (and therefore sacrificing parallelism) we could use a constant number of pointers across merge sort, meaning the space complexity can be as low as O(1). However, in a recursive implementation we are more likely to be using O(log(n)) space as we will need to create several pointers to keep track of our current list at each step.
Problem 4
When we recurse, rather than calling a function in our code, we can instead dispatch that code to run on another computer or as a subprocess. Provided the other function has the ability to modify the existing array, either by sharing memory space in the case of threading, or by having access to some shared disk, the code should run recursively without much issue.
Since each machine would be doing one operation (comparing two numbers) you will need n/2 machines or cores to do this.
A more realistic use of this is to limit each machine to some sublist length, say 1024 elements, and distribute the work to as many machines as needed for the number of elements we're working across.