After writing the lexer I could turn any math expression into a set of tokens. However, they were still organised as a list and couldn't be used to do any useful work. To go from a list of tokens to a program, I needed to write a parser.

The goal for any parser is to output a parse tree. A parse tree is a type of data structure which organises an expression in a way the computer can use to generate a list of simple operations. If we want to compile our expression, then this will be machine code; if we want to use an interpreter, it will be a set of functions in our interpreter. Parse trees look something like this:

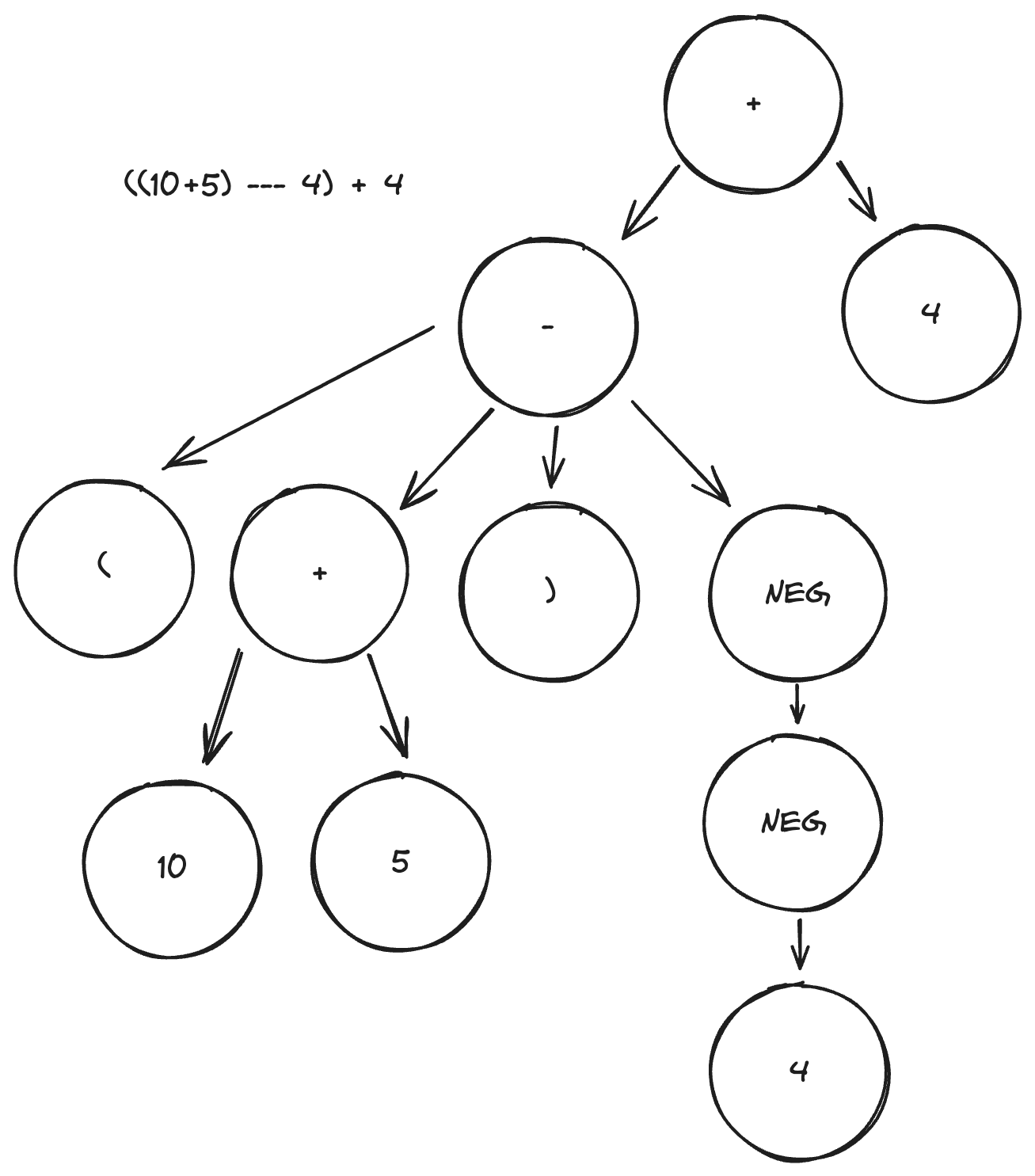A parse tree representing the equation.

Parse trees can be verbose, so we often use one more step to reduce them to an abstract syntax tree, which is easier for the computer to use. Abstract syntax trees (ASTs) look like this:

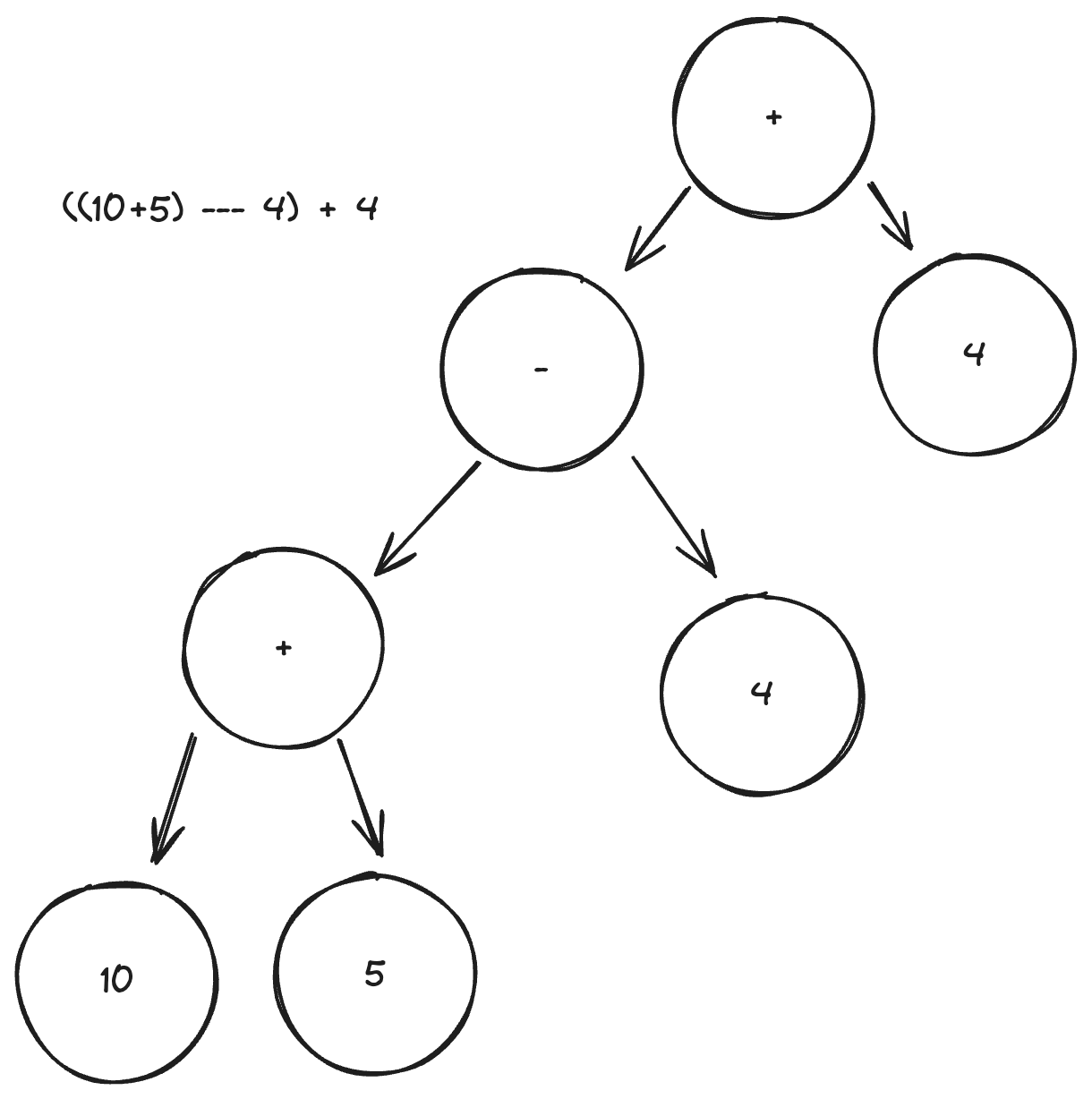An AST for the same equation. Notice that all unnecessary elements have been removed from the tree.

An operator-precedence parser is a simple type of shift-reduce parser. Shift-reduce parsers work bottom-up - they go through a list of tokens and attempt to build a tree by grouping tokens together. In the case of an operator-precedence parser, this is done by checking different operators in order of precedence.

In algebra our operations are, in order:

• Expressions in parentheses: (x+2)
• Exponentiation: x^3
• Multiplication and division: x*3 or x/2
• Addition and subtraction: x-2 or x+3

An operator-precedence parser will check each of these in order and organise tokens accordingly. Note that as addition and subtraction are the same operation, they are simply read left-right. The following example shows how this process works step-by-step.

10 + 10 ^ 3 / 5 * 3
// skipping parentheses, try exponentiation
10 + (10 ^ 3) / 5 * 3
// exponentiation done, try divide and multiply
10 + ((10 ^ 3) / 5) * 3
10 + (((10 ^ 3) / 5) * 3)
// divide and multiply done, try addition and subtraction
(10 + (((10 ^ 3) / 5) * 3))
// expression completed!

This is equivalent to the following abstract syntax tree:

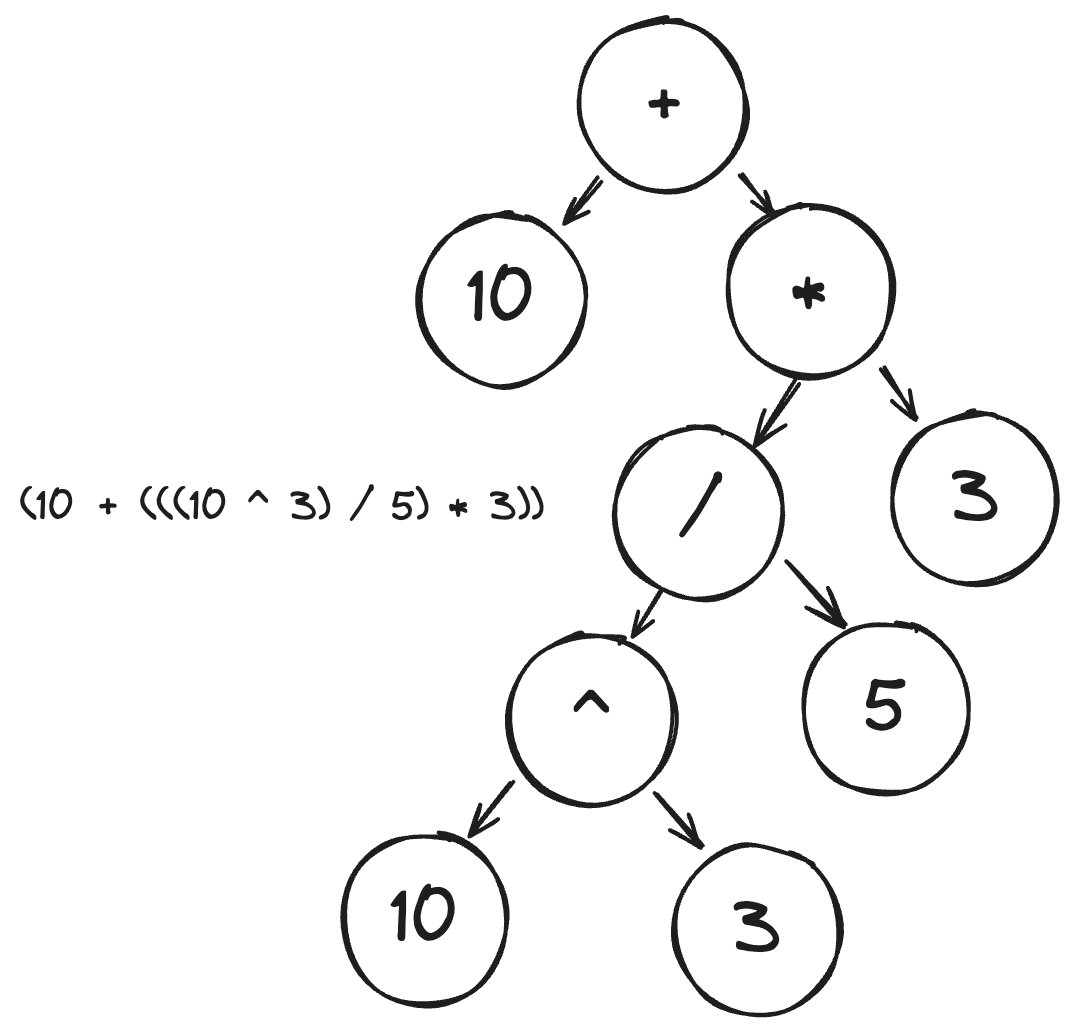
You can represent this tree however you like in memory: however, my preference is as a nested list. (Note that in C an n-ary tree and a nested list are identical.) In Python our algorithm looks like:

# this is an incomplete and probably buggy piece of code
# it's just designed to demonstrate bottom-up parsing
# and its general algorithm
# a full implementation would include the NEGATE operand, for example 

def nest_operation(op_str: str):
   def out_fn(tokens: list[str]):
        new_tokens = []
        for i, token in enumerate(tokens):
            if token != op_str:
                new_tokens.append(token)
                continue
            new_tokens.extend( [tokens[i-1], token, out_fn(tokens[i+1:])] )
            return new_tokens
    return out_fn

def make_parse_tree(tokens):
    cur_tokens = deepcopy(tokens)
    for operand in ("^","/","*","+","-"):
       parse_fn = nest_operation(operand)
       cur_tokens = parse_fn(cur_tokens)

The basic idea is that we're iterating through the list of tokens as many times as there are operands and grouping together tokens based on the priority of each operand. This is what makes this a shift-reduce parser - we shift along one token at a time, and reduce 3 tokens at a time to a single operation.

With the parsing algorithm complete, all that was left to do was make the AST do some useful work. The first thing I wrote was an interpreter in Python:

def evaluate(node):

    ops = {
        '^' : lambda x, y : x ** y,
        '+' : lambda x, y : x + y,
        '/' : lambda x, y : x / y,
        '*' : lambda x, y : x * y
    }

    if isinstance(node, str):
        return float(node)

    elif isinstance(node, ParseNode):
        if node.token in adme:
            left = evaluate(node.children[0])
            right = evaluate(node.children[1])
            return ops[node.token](left, right)

    elif node.token == minus:
        return evaluate(node.children[0]) * -1

It's only 20 lines! Building up the parse tree is the more difficult part of the code.

The interpreter goes through the parse tree starting from the root and checks the children of each node. When it reaches a number, it returns that number as a float. It then climbs back up the parse tree until it's performed all the math necessary. You can look at this as the reverse of our previous process of building the tree:

(10 + (((10 ^ 3) / 5) * 3)) // evaluate 10 ^ 3
(10 + ((1000 / 5) * 3)) // evaluate 1000 / 5
(10 + (200 * 3)) // evaluate 200 * 3
(10 + 600) // evaluate 10 + 600
610

After writing the interpreter, I was curious if I could turn it into a compiler. This was a bit more difficult, but still simpler than writing the parser itself. By using a similar process to the interpeter, I turned my parse tree into the LLVM intermediate representation language (IR). This is a special assembly language which can compile to many different CPU and operating system combinations. It looks like this:

@.str = private unnamed_addr constant [3 x i8] c"%f\00", align 1

declare i32 @printf(i8*, ...)

define i32 @main() {
    %x1 = fadd float 4.0, 5.0
    %x2 = fmul float 2.0, %x1
    %x3 = fdiv float %x2, 3.0
    %x4 = fpext float %x3 to double
    %x5 = call i32 (i8*, ...) @printf(i8* getelementptr inbounds ([3 x 
            i8], [3 x i8]* @.str, i64 0, i64 0), double %x4)
    ret i32 0
}

You'll notice that lines 6-8 describe basic math operations such as adding, multiplying, and subtracting - this code follows the same logic as the previous example, albeit in a much more verbose way.

The most important principle when writing assembly or intermediate representations like LLVM is to use static single assignment form. In most languages you can assign to a variable more than once. For example, in C you could write the above assembly as something like:

float x = 4.0f + 5.0f;
x = x * 2;
x = x / 3;
printf(x)

However, in LLVM IR you can't modify variables which you've already declared. Instead of using a single variable called x we need to keep multiple versions, which are labelled as %x1 and so on in the code above.

Once I'd generated LLVM from my math, all I needed to do to get a binary program was run the llvm and clang compilers on them, then...

chmod +x math
./math
6

Moving On Up

I'd written a basic math parser and compiler, but being limited to one-line math expressions is no fun. I wanted to add a few features to build a new language, Infix Plus:

• Multiple lines in the program
• Python-style comments, # written like this.
• Assigning variables like this a = 10, the same way as Python
• Being able to use variables in expressions and get a result: a + b + c

To get there I'd need to learn more about how formal grammars work and a new type of parser: recursive descent.